看了Evaluation of failure probability via surrogate models，记录一下。
针对失效概率估计的代理模型主要是得到一个
失效概率可以定义为积分的形式：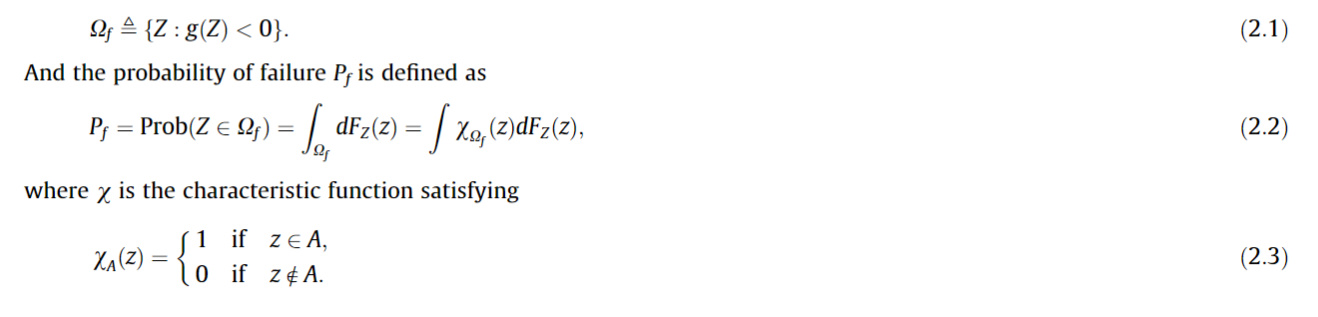
论文的贡献点：
- demonstrate that the straightforward sampling of a surrogate model can lead to erroneous results, no matter how accurate the surrogate model is.
- propose a hybrid approach by sampling both the surrogate model in a ‘‘large” portion of the probability space and the original system in a ‘‘small” portion
convergence
关于第一个直接对于不管其精度有多高，代理模型进行采样会导致错误的结果是通过例子来论证的，这说明在使用代理模型进行计算时，即使它们在大多数点上的值非常接近，也必须非常小心，因为在某些关键的性质上，它们可能给出错误的预测。
- 局部误差的放大：在对函数进行积分时，局部的小误差可能在整个积分区域内累积，导致总误差较大。
- 模型的非线性：非线性系统可能对输入的微小变化非常敏感，因此即使是非常接近的两个模型，其输出也可能大不相同。
- 极值或尾部行为：对于系统的某些性能指标，可能更依赖于输入分布的极值或尾部行为，而这些区域的模型逼近可能不够准确。
就算不是仅仅偏向于一个边的也会出现这个问题：
上面的Gibbs’ oscillation。具体来说，当用三角函数的有限和（例如，傅立叶级数的前N项）去逼近一个有跳跃不连续性的周期函数时，在跳跃不连续点的两边，逼近函数会出现波峰和波谷，这些波峰和波谷不会随着N的增加而消失，尽管它们的宽度会随着更多的项被加入而变窄。
hybrid approach
- 得到近似：
（可以用不同的方式得到） - 设置
, 当 足够接近于0，也就是临界状态的时候采用
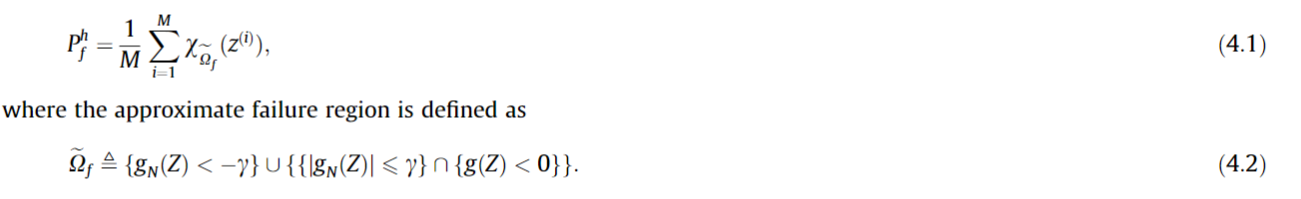
其中临界值
证明
收敛性证明：
首先证明了概率和拟合程度之间的关系：
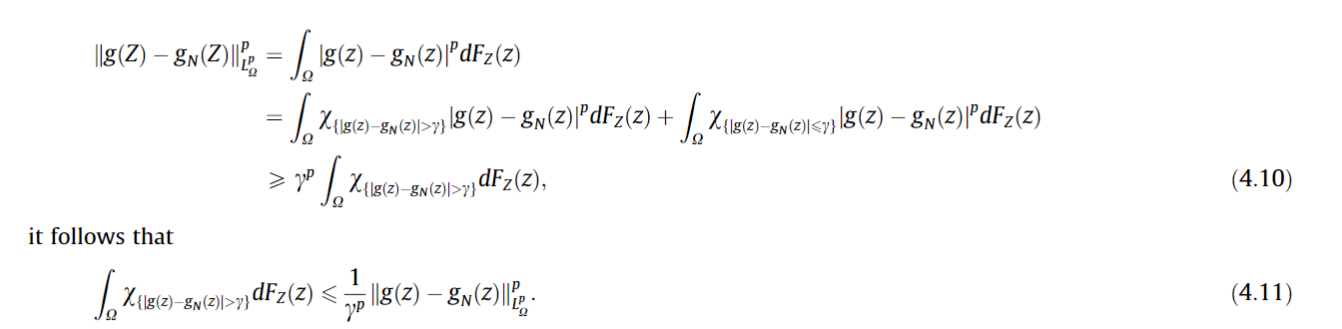
证明 收敛性 夹逼定理：
之后就可以通过MC方法来估计$P{(N,\gamma)}
但是这个不容易估计
迭代方式
初始化的时候从Z中采样生成M个点，之后根据这M个点估计一个
迭代的时候，选择前面
上面的部分右侧部分加上的东西就是，将原始