Polynomial Chaos

看了 Polynomial Chaos: A Tutorial and Critique from a Statisticianís Perspective, 总结一下：

uncertainty quantification：主要研究的是不确定的传播。Given input x, the simulator produces output . Typically, both x and y are vectors. Letting the input be uncertain, we represent this with a random variable X, in which case the output is also a random variable

一般从下面两种方法进行：

1. 一种是MC的方式，从X中采样得到大量的点之后，通过去进行模拟去刻画Y的分布
2. 更普遍一点的方式是构建代理模型，这个模型在足够接近的同时还能够高效的进行采样

针对这个问题，在AM(applied mathematics and …)中经常使用Polynomial chaos expansion，而在Stat(statistics)中则经常使用Gaussian process emulator

PCE

PCE: way of representing an arbitrary random variable of interest as a function of another random variable with a given distribution

将一个随机变量表示为给定分布的随机变量的函数（多项式展开）

$$X=f(\Xi)$$

其中X是一个随机变量，是来源于另外一个分布的随机变量，在PCE的背景中称之为germ，germ分布一般是比较容易采样的分布，这样做之后复杂的随机变量就容易采样了

一些理解性的例子

上述表示不仅仅是可行的，而且往往还有很多种方程能够实现这个事情：比如说可以通过逆变换的方式将均匀分布的随机变量转化为其他分布的随机变量。下面是一个更加广泛的例子：

大致意思是，将X和Y都分解为多个segment，每个segment都能各自对应上去，也可以任意确定之间对应的关系，对应关系的选法有 种。

下面的例子则进一步表示，每个随机变量通过不同类型的函数变换，但是得到的分布可以相同

CDF是单调的，对应的Inv-CDF也是单调的。但是对应的平方不是，所以这是两个不同的方法
可以有以及$X=Fx^{-1}(F{\xi}(\Xi))$两种不同的转换方式，但是两种方式得到的X可以服从同一种分布

一元的情况

这部分介绍一元的表示，PCE就是将中的函数进行正交多项式展开，其中正交的选取是选择germ分布对应的正交多项式（germ分布要求其各阶矩都有限，不然也定义不了无限阶的多项式了）：当时：

$$\langle \psi_j,\psi_k\rangle=\int \psi_j(\xi)\psi_k(\xi)p_\xi(\xi)d\xi = 0$$

使用正交基可以将函数表示为下面的形式：

$$X=f(\Xi)=\sum^{\infty}_{j=0}x_j\psi_j(\Xi)$$

其中 一般来说都会只取前面p阶多项式，不会取到无穷项

正交性带来的第一点是：各个正交基的均值是0 因为 ，其次由方差的公式可知均值为0的时候对应的就是方差, 对应的就是协方差

三种不同的germ下面的正交基 常见于三种不同的情况（有界、半无限，无限）：

问题

所以为了得到还需要得到的表示形式，这个就比较难办了:

The next step is to devise a suitable representation function f . Several examples have been given to show that this is always possible and moreover that there will always be many solutions. In practice, though, apart from the general solution (2) it will not be straightforward to Önd representations. Considerable research e§ort has in the past been spent on e¢ cient ways to sample from given distributions using uniform pseudo-random numbers, but many good sampling methods are iterative or implicit and I cannot see how those could be adapted for PC representations. Even the CDF solution requires the CDF of X to be known explicitly, which may not always be the case in practice. [[Polynomial-chaos stat perspective.pdf#page=7&selection=0,0,20,63]]

就算是 已经知道的情况下，也要算个积分 这个也没有那么好计算得到
还有 像是之前讨论过的 只是 并不能说明转换之后的分布是一致的：

In practice, this is achieved in the usual way by increasing p until the mode weights appear to stabilise and new weights are small. However, this is really assessing whether fp approximates well to f , and does not guarantee that the distribution of Xp approximates well to that of X. [[Polynomial-chaos stat perspective.pdf#page=7&selection=76,55,99,1]]

多元的情况

大多数情况下 以及 都是向量。
如果是向量的话对应的每个模态的权重也要是向量

如果是向量的话，多项式也需要是多元的可以记作, 特别是当中都是独立的时候，是各个多项式基的张量乘积

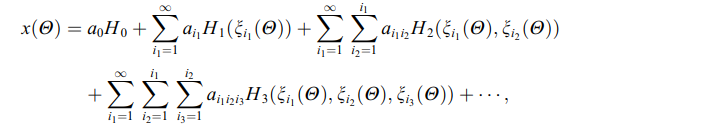
当有一个$\Xi = (\xi1, \xi_2, …, \xi_n)\Psi(\Xi) = a{i_1,i_2,…,i_n}\xi^{i_1}_1 \xi^{i_2}_2 … \xi^{i_n}_n$

如果中的元素是独立的，那么多项式基的张量乘积指的是这些基函数相互独立组合的结果。在多项式空间中，基函数是构建多项式的基础块。对于多元情况，每个变量有自己的基函数集，张量乘积就是从这些集合中各取一个基函数，然后将它们相乘得到一个多项式基。

例如，如果对于两个变量 x 和 y 的二元多项式，基函数集分别是 和 ，那么张量乘积会得到一组二元多项式基 。

张量乘积对于多项式来说是基向量的扩展，两组正交基的张量乘积表示的是两组的扩展空间
当有index：$j = (j1, j_2,…, j_m)\Psi_j(\xi)=\prod{i=1}^{m}\psi_{j_i}(\xi_i)$

当实际应用的时候是被truncated 到P阶的，所以对于上面这个表达式又有
这个时候对于m维，总阶数为p的index的设置，相当于将p阶分配在m维度中，并且允许某个维度没有阶数，可以转化为组合数学中的隔板法，具体的证明方法可以看前面给出的链接。

得到的结论是所有的组合个数是，然后又有：

$$\sum^p_{r=0}\begin{pmatrix}m+p-1 \\ p\end{pmatrix}=\begin{pmatrix}m+p \\ p\end{pmatrix}$$

这个东西大致的增长速度大概是m的p次方，因为，p一般不会很大，所以忽略分母的同时上面的部分也近似

Propagation

主要是对计算模型的结果进行PCE展开

Y = η(X).模型可以写成这种形式，Y以及X一般来说都是随机向量，PCE一般是将Y以及X都做相同阶数的展开：

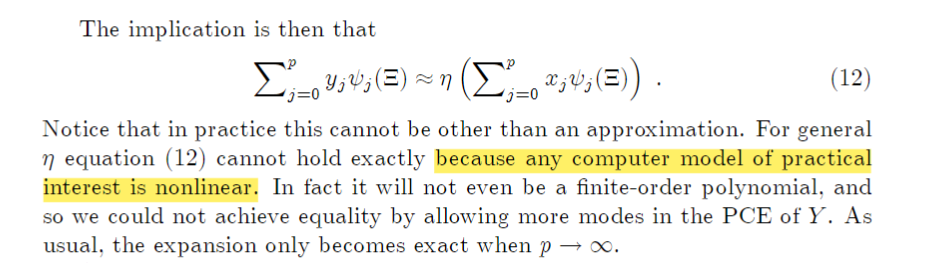
实际中的计算机模型通常是非线性的，因此方程(12)不能“完全成立”，即不能精确地描述这些模型。因为非线性模型包含了复杂的变量相互作用，这些作用不能简单地用有限阶的多项式来捕捉。所以为判断近似是否充分 一般是逐步增加阶数p知道每个mode的strength变化的很小为止

I believe it is fair to say that the PCE approach does not quantify the approximation error as a compo- nent of uncertainty：[[Polynomial-chaos stat perspective.pdf#page=10&selection=199,56,201,19]]

之后核心的部分主要是估计上面公式12中的，具体的估计分为两种方法intrusive以及non-intrusive

Intrusive

Galerkin projection 是一种数值方法，用于将连续问题（通常是微分方程）转化为离散问题（通常是代数方程），这样就可以在计算机上求解。这种方法是有限元方法的核心：

1. 问题的连续形式：开始时，你有一个连续的问题，通常是一个边值问题或一个初值问题，它由微分方程和边界/初值条件定义。

2. 选择基函数和测试函数：选择一组基函数（也称为试验函数）来表示解的近似，以及一组测试函数来检验这个近似。在有限元分析中，基函数通常与网格单元相关，而测试函数是基函数的副本。

3. 投影到近似空间：将微分方程中的每一项都用基函数展开，然后通过测试函数的加权积分将问题投影到近似空间中。这个过程会生成一个系统的代数方程组。

4. 求解代数方程组：最后，通过求解这个代数方程组来得到近似解。

在数值方法中，将 PCE 结合 Galerkin 方法用于随机微分方程，通常被称为随机 Galerkin 方法。这种方法要求在数值求解微分方程时对方程进行修改，将不确定性直接包含在方程中，这是一种侵入式的方法。这与直接在求解器中加入随机性的非侵入式方法（如蒙特卡洛模拟）相对。

具体方法式将Y以及X的展开带入到方程之中，用p个基函数对其求内积，离散成p个方程组，之后求解。

缺点就是需要手动化简之后再编程进行求解，并且对于不同阶数有不同的情况。而且很多时候Y以及X的基函数选择可能会很不一样，所以上面的化简也会更麻烦

Non-intrusive

就是在方程（求解器）之外加入随机性，主要有两种Monte Carlo以及Regression两种方式：

MC

非侵入式的方式就是用上面的形式直接求解，上面的积分问题要么转换为MC去做，要么使用quadrature rule：

1. 矩形规则（Rectangular Rule）：这是最简单的求积方法。它通过将积分区间划分为多个小区间，然后在每个小区间上用矩形的面积来估计函数下的面积。根据所选择的点（左端点、右端点或中点），矩形规则可以进一步细分为左矩形规则、右矩形规则和中点规则。

2. 梯形规则（Trapezoidal Rule）：在每个小区间上，梯形规则使用梯形而不是矩形来近似函数下的面积。这通常比矩形规则更精确，因为它考虑了函数在区间两端的值。

3. 辛普森规则（Simpson’s Rule）：辛普森规则通过将每对小区间上的函数近似为二次多项式，然后积分这个多项式来提高精度。它基于三点（区间的两端点和中点）上的函数值，比梯形规则通常更精确。

4. 高斯求积（Gaussian Quadrature）：这是一种更高级的方法，它选择特定的点和相应的权重来优化积分的近似。高斯求积通常能在少量计算点的情况下提供非常高的精度。

   Monte Carlo typically requires a large number of simulator runs, which is impractical for computationally-intensive models, but on the other hand in higher dimensions, tensor products of quadrature rules demand even more simulator runs. Although sparse quadrature rules exist and are more e¢ cient, still quadrature seems impractical when the germ vector is high-dimensional [[Polynomial-chaos stat perspective.pdf#page=13&selection=2,0,6,76]]

Regression

另外一种方式是将其看作回归模型：

Regression is a common way of building a surrogate model and polynomials are the commonest regressor variables for this purpose. Using or- thogonal polynomials helps with the numerical stability of the computations, but orthogonality then needs to be with respect to the empirical distribution of the design points, rather than with respect to the germ distribution. Using PC o§ers no advantages that I can see. [[Polynomial-chaos stat perspective.pdf#page=13&selection=97,0,102,29]]

这个好像意思是使用回归的时候和正交多项式回归没有什么区别